A. 角数は30くらいが上限
理論的には正多角形の頂点となる角数に制限はありませんが、限りなく円に近くなってしまうので、30角くらいを上限にしています
また、正多角形をモチーフにしているのは、角数の拡張を簡単にできるようにするためです
例えば、正5角形の描画で決めたルールを応用できれば、角数を増減するだけで、比較的簡単に、正7角形や正9角形を描けるようなります
コマを繰り返し描いていく
ここでいうルールとは、多角形の一つの頂点を中心とする頂角の範囲に描く基本図形(コマ)の描き方です
具体的には、コマを構成する節点の位置が、多角形の中心点から、どの方向にどのくらい離れているか、その場所を正確に把握したうえで線をつないでいくということです
コマ同士は一定の角度(360度÷角数)の倍数で回転した位置関係にあるので、最初のコマの各節点の位置が分かれば、それぞれの頂点の位置に応じた角度を使って回転させれば、相応の節点の位置を決めることが出来ます
節点の位置は座標として指定する
それぞれのコマの各節点の位置は、コンピューターで描く場合では、画面の左上から、横方向と縦方向のそれぞれがどれだけ離れているか、その距離を計算し座標として指定します
最初のコマを構成する節点の座標を求めることが出来れば、その他のコマの節点は頂点の位置に応じて、正多角形の中心点を基準に回転することによって求められます
例)コマを回転してつなげるイメージ
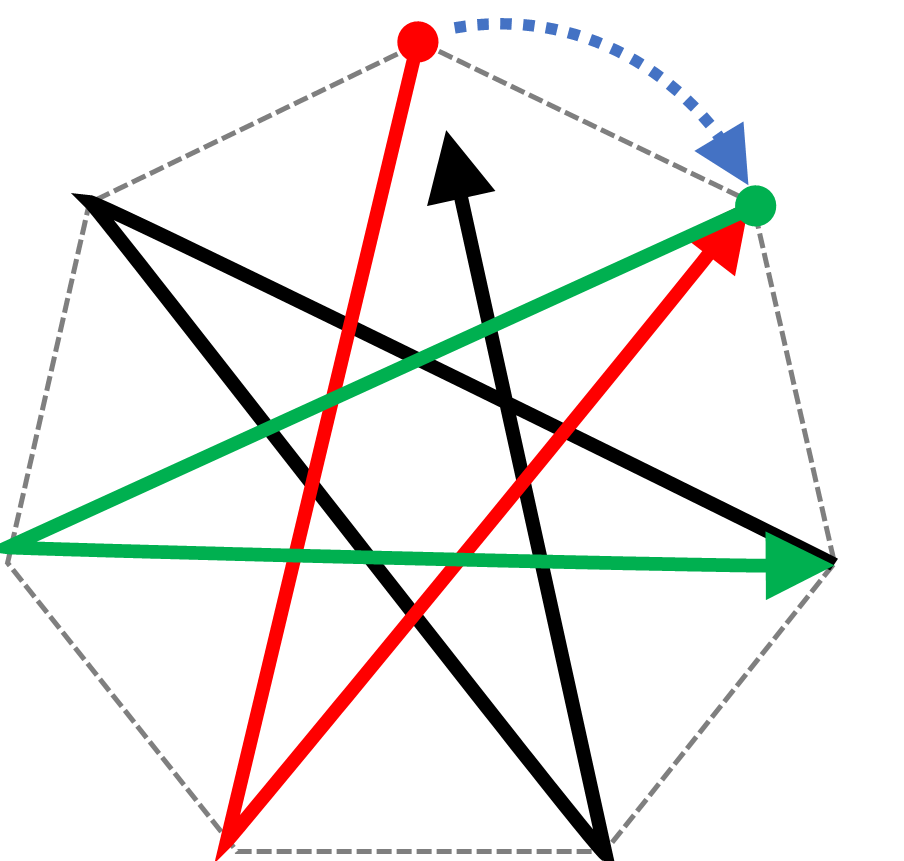
最初のコマ(赤の線)を描いたら、このコマを360÷7度時計回りに回転させて、赤の線の終点を始点とする次のコマ(緑の線)を描きます
角度が分かっているので、サイン・コサイン・タン…を使って、それぞれの節点の座標を求めることが出来るわけです
素数の魅力
角数について、多くても30角くらいという話をしましたが、その中でも、奇数の角数を好んで描いています
左右対称に描いたとき、上端と下端の違いから安定感が得られるからです
5角形の星型と6角形の星型で安定感を比べてみましょう

何となく、5角形の方がドッシリしてますね
なかでも素数が好き
その中でも、素数が気に入っています
7、11、17、19、23などの角数を持つ多角形をモチーフにした図形です
6角形や8角形などは、三角形や四角形を重ねたり、くり抜いたりして描くこともできるのですが、素数の多角形となると、ひとつずつコマを描いて行かなければならないので、その難しさがかえって夢中にさせる所以かもしれません
もちろん、偶数でも描きます
特に、隣同士の頂点の位置を少しずらして、大き目のコマと小さめのコマが互い違いになるようにしたい場合には、偶数である必要があります
ただこの場合でも、例えば7の2倍の14角や、17の2倍の34角などの角数をよく使います
また、3の9倍の27角なども面白いです

コマをパターン化して多角形全体に埋め込むような場合、これは和柄をモチーフにした図形の場合が多いのですが、この時には偶数の角数もよく使います