
星型の作品として紹介した【star005】をサンプルとして、骨格となる描線(フリーフォーム)を描く工程を説明します
編集したり、色を入れる前のフリーフォームは表計算ソフト(エクセル)を使って描いているので、このページではそれぞれの作業をエクセルで行っている前提で説明していきます
図形の場所を座標として認識する
エクセルでは表(シート)に図形を描くことが出来ますが、その位置や大きさは座標として認識します
座標の二つの要素(X座標、Y座標)は表の左上隅から、それぞれ右方向と下方向への距離で指定します
単位はポイントを使います(72ポイント = 1インチ ≒ 2.54センチ)
作業手順
- 台紙を用意する
- 基本的な図形(コマ)を折れ線で台紙上に描く
- コマの線分を直線から曲線に変形する
- 多角形の頂角に応じたコマを連続してつなぎ、全体を『一筆書き』で描く
1. 台紙を用意する
図形を手書きで描く時に方眼紙を使うと、長さや相対的な位置の関係を把握し易いように、多角形をモチーフにした図形用に、方眼紙に相当する円盤状の台紙を用意します
ア)図形の中心の座標を決める
まず、シートの何処に図形を描くのか、その基準となる座標を決めて、その座標を台紙の中心に指定します
このサンプル(star005)ではX座標、Y座標共に380ポイントを中心の座標として指定しています
これによって、台紙の半径を300ポイントとした場合、上と左に80ポイントの余白を設けることができます
イ)主軸を描く
モチーフとする多角形の頂点と台紙の中心を結んで放射状の主軸を描き、時計の12時を基点に軸記号を割り当てます
このサンプルは7角形を原型としているので、a0からg0の記号を割り当てます
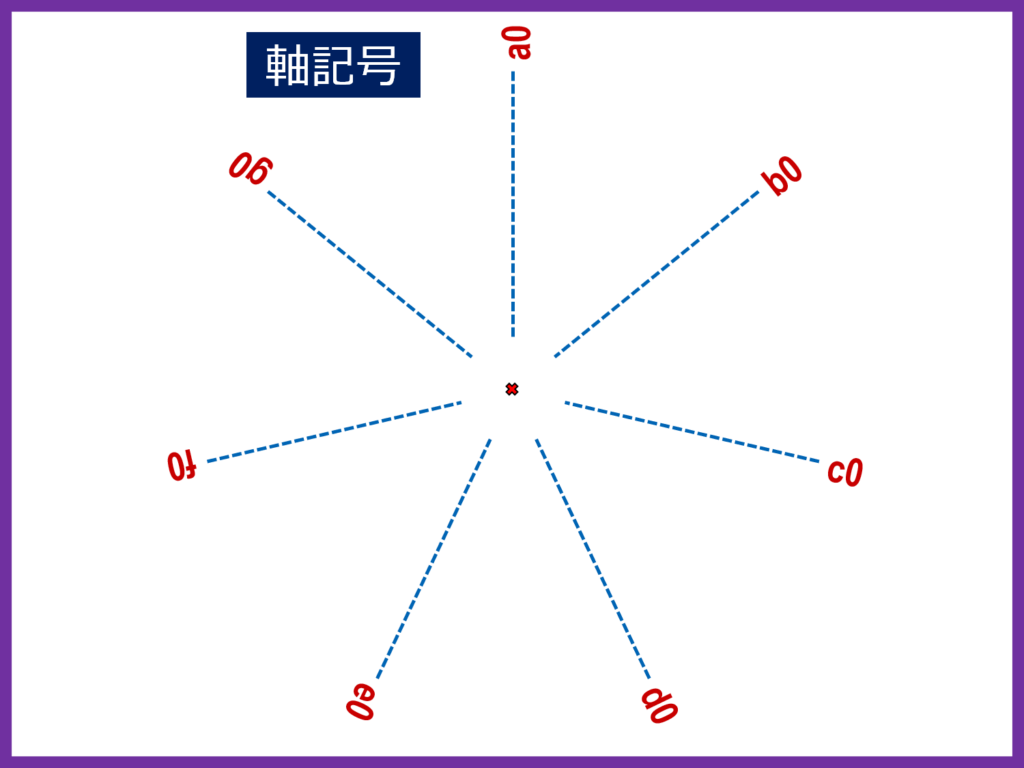
ウ)補助軸を描く
主軸だけでは足りないので補助軸を描き、同様に軸記号を割り当てます。同じ頂角の補助軸は主軸のアルファベットに1から始まる連番を付けて軸記号とします
補助軸の本数は描きたい図形の節点の数に応じて任意に設定します
このサンプルでは各頂角に主軸、補助軸併せて8本の軸を設定してあります

エ)同心円を描く
軸が方眼紙の縦線とすると、横線が必要になるので、同心円を描きます
一番外側の同心円は台紙の輪郭に相当し、このサンプルでは半径300ポイントの円になります
その内側に2番目の同心円を描きますが、その半径は外側の同心円で隣り合った軸によって区切られた円弧の長さだけ短くした長さにします
そうすることによって、軸と同心円で囲まれる格子が正方形に近いイメージに仕上げることが出来ます
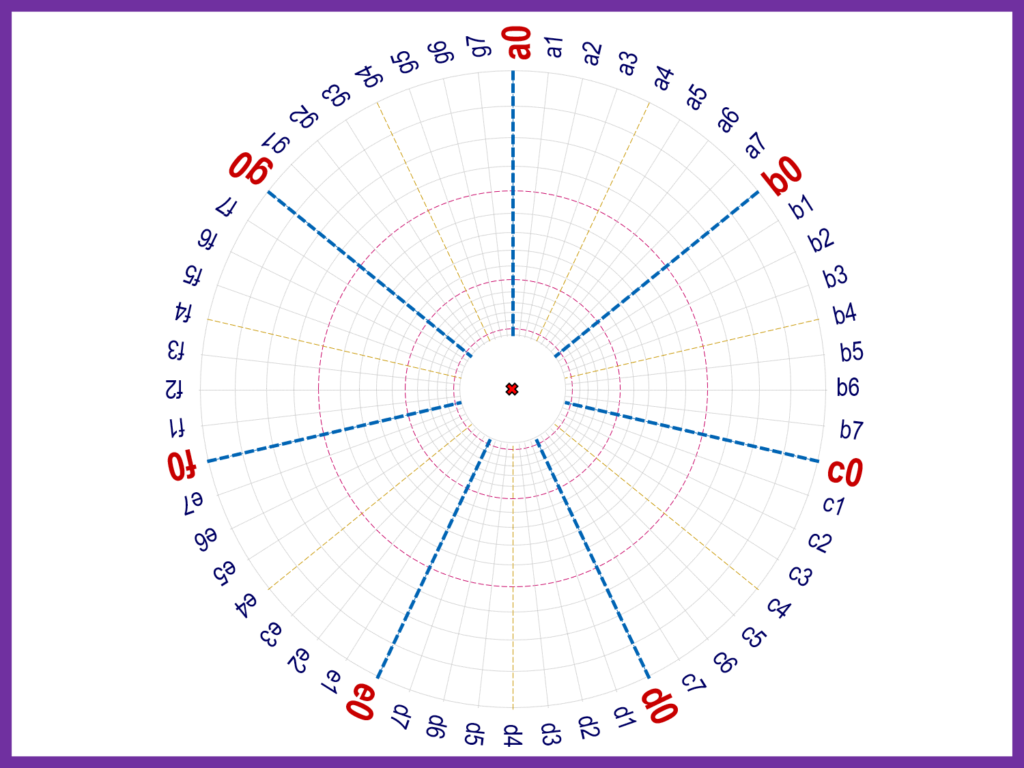
なお、台紙の中心部分は密集して図形の描画が出来ないので、同心円の半径の最小値を50ポイントにしています
オ)同心円に径位置を割り当てる
外側の同心円から順番に1から始まる整数を径位置としてを割り当てます
5の倍数の径位置の同心円は線のスタイルを変えて判別し易いようにします
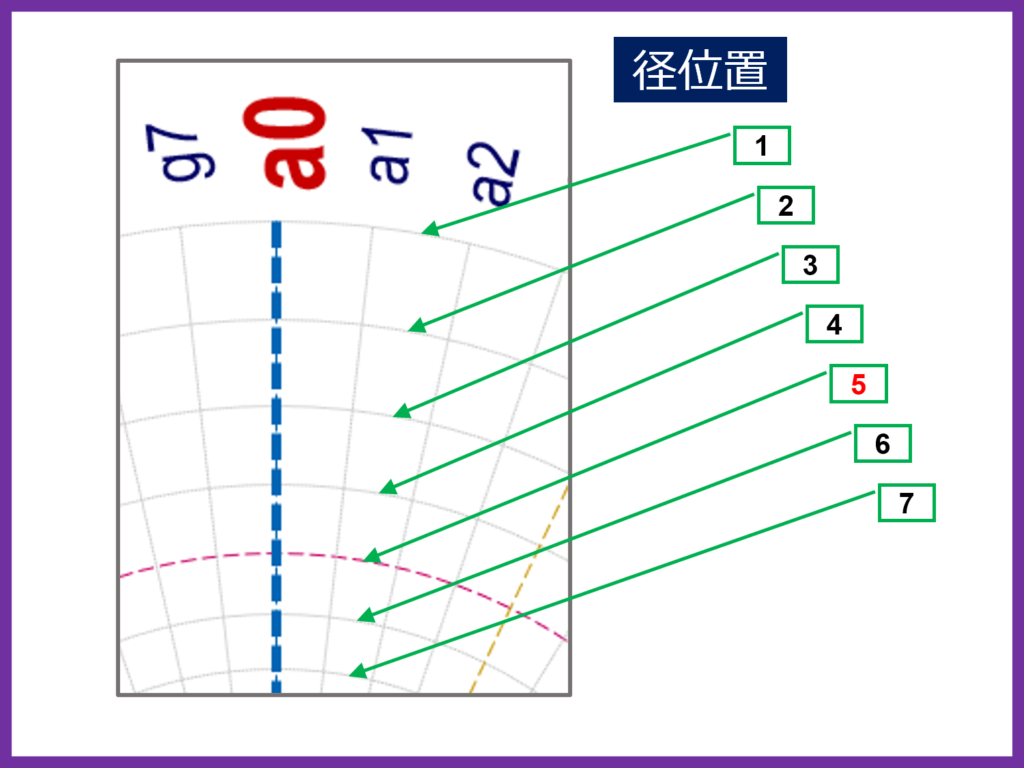
カ)台紙の使い方
このサンプルでは7×8=56本の軸と、16個の同心円を配置した台紙を用意したので、都合896ヶ所の交点(軸記号と径位置の組み合わせ)から描きたい図形の節点を選ぶことが出来ます
微妙なカーブを付けたい時に交点がうまく見つからない場合には、軸と同心円の数を増やした台紙を用意すれば、意に沿った図形を描くことが出来るようになります
2. 基本的な図形(コマ)を折れ線で台紙上に描く
台紙が用意できたら、その台紙の上にコマとなるフリーフォームを折れ線で描きます
ア)ツールでフリーフォームを描く
エクセルでシート上にフリーフォームを描くには、開始点から始めて節点を任意の場所にプロットしながらつなげて描いていくのですが、節点の座標を厳密に指定して描くために、フリーハンドではなく、マクロを使ったツールを作成して描いています
詳しいプログラミングの説明は割愛しますが、キーとなるスクリプトは以下のように、指定した座標情報に従って節点を順番につなげているので、描画の手順はフリーハンドと同じです
Shapes.BuildFreeform(開始点の座標情報)
Shapes.BuildFreeform.AddNodes(2番目の節点の座標情報)
Shapes.BuildFreeform.AddNodes(3番目の節点の座標情報)
Shapes.BuildFreeform.AddNodes(4番目の節点の座標情報)
…
Shapes.BuildFreeform.ConvertToShape
2行目から最後の行の手前まで、節点の数だけ指示を繰り返します
イ)座標の求め方
パラメーターとなる座標をどのように取得するのか、サンプルとして【軸記号:a3、径位置:2】の交点を節点として指定した場合のY座標の求め方を説明します
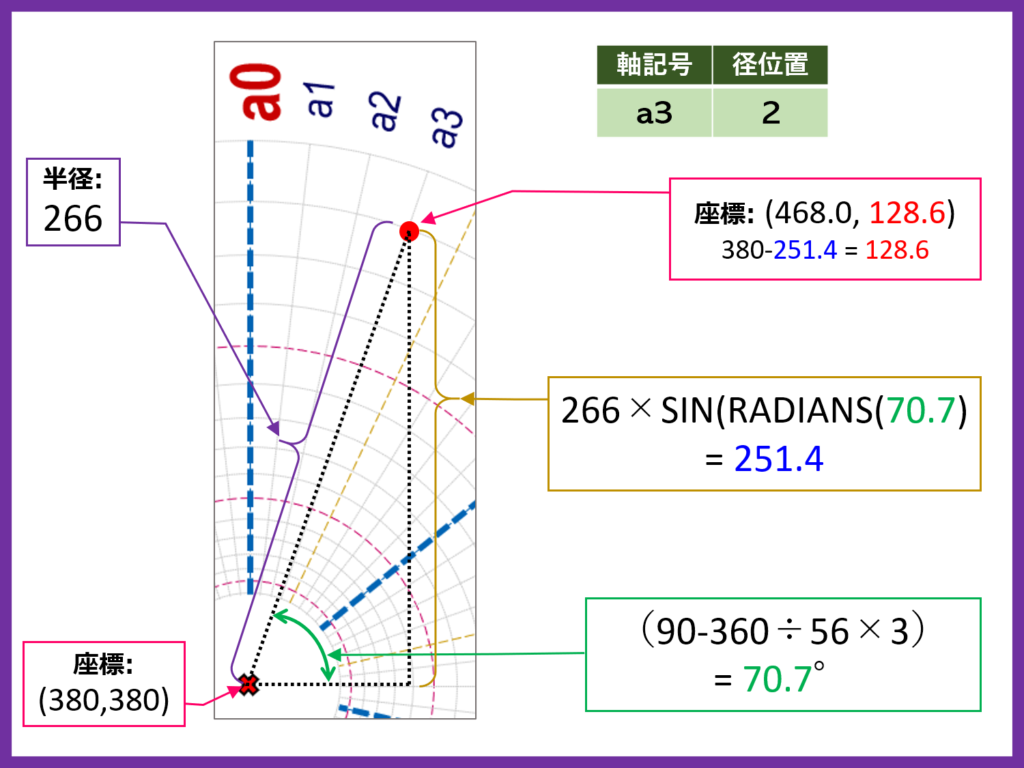
この節点の中心からの長さは300-300×2×パイ÷軸の総数(56)=266ポイント、a3の補助軸はa0から3番目に位置しているので、この軸の角度は90-360÷軸の総数(56)×3=70.7度、これらを三角関数(サイン)を使って計算するとこの節点は中心から251.4ポイント上に位置していることが分かります
中心のY座標は380ポイントなので、この高さを引いた128.6ポイントがこの節点のY座標になります
同様にコサインを使えばX座標を求めることが出来ます
ウ)コマを描く
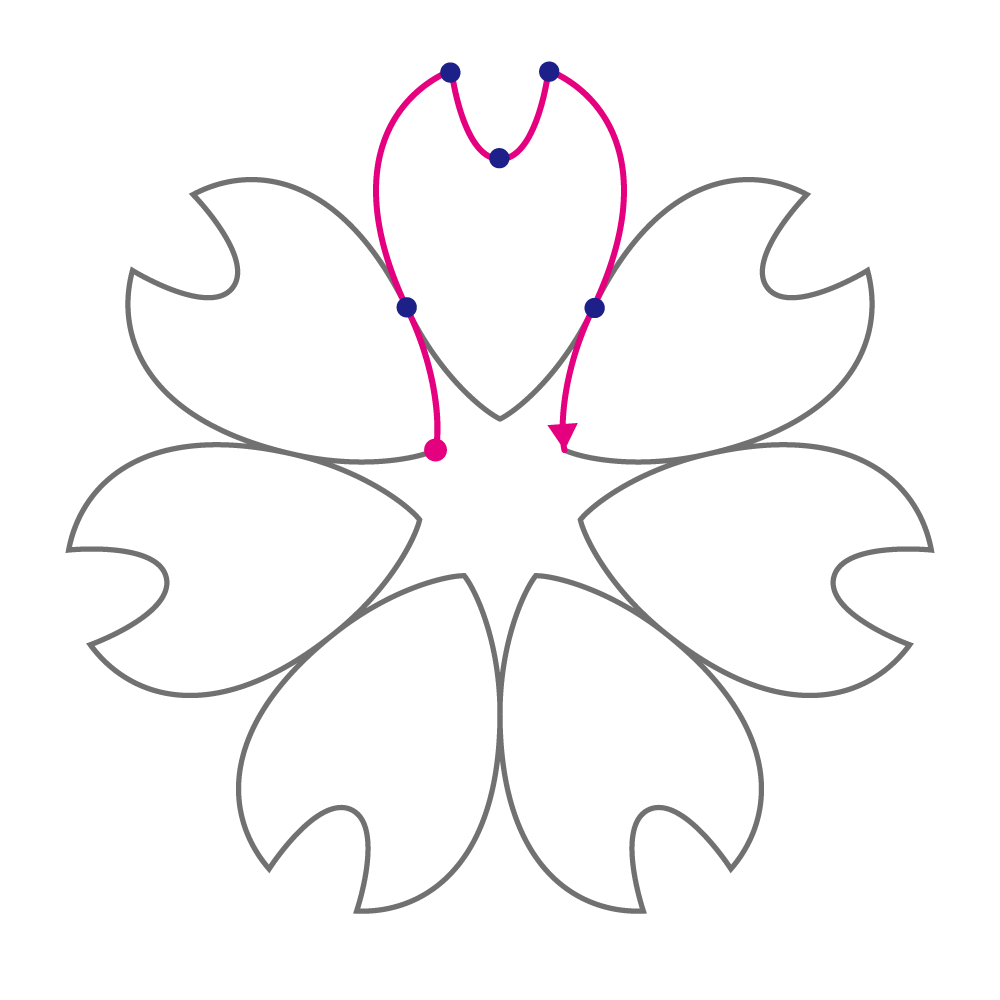
サンプルの図形には全部で42個の節点がありますが、基本図形のコマ(ピンクの線)の節点は7個です(開始点、青い点×5、終了点)
この7個の節点の軸記号と径位置を描画する順番に並べてまとめておきます
具体的には、下記のような入力フォームを使っています
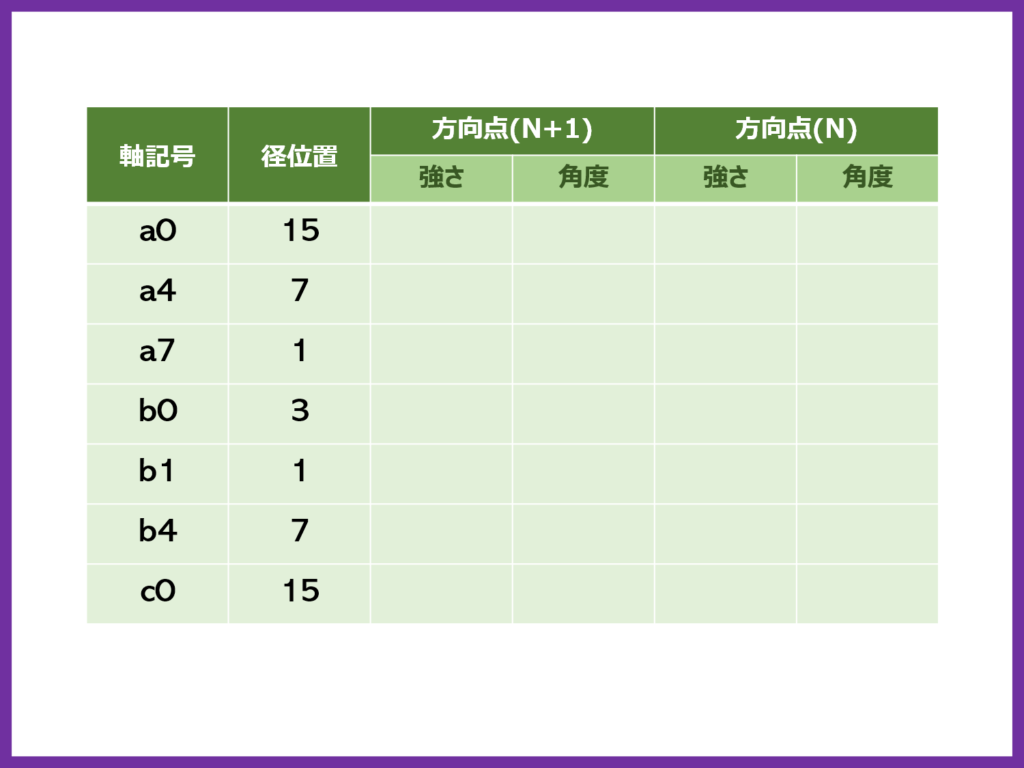
方向点に関する情報は線分にカーブを付ける時に必要な情報なので、この段階では使いません
節点の座標情報を反映したフリーフォームは折れ線の図形として描画されます
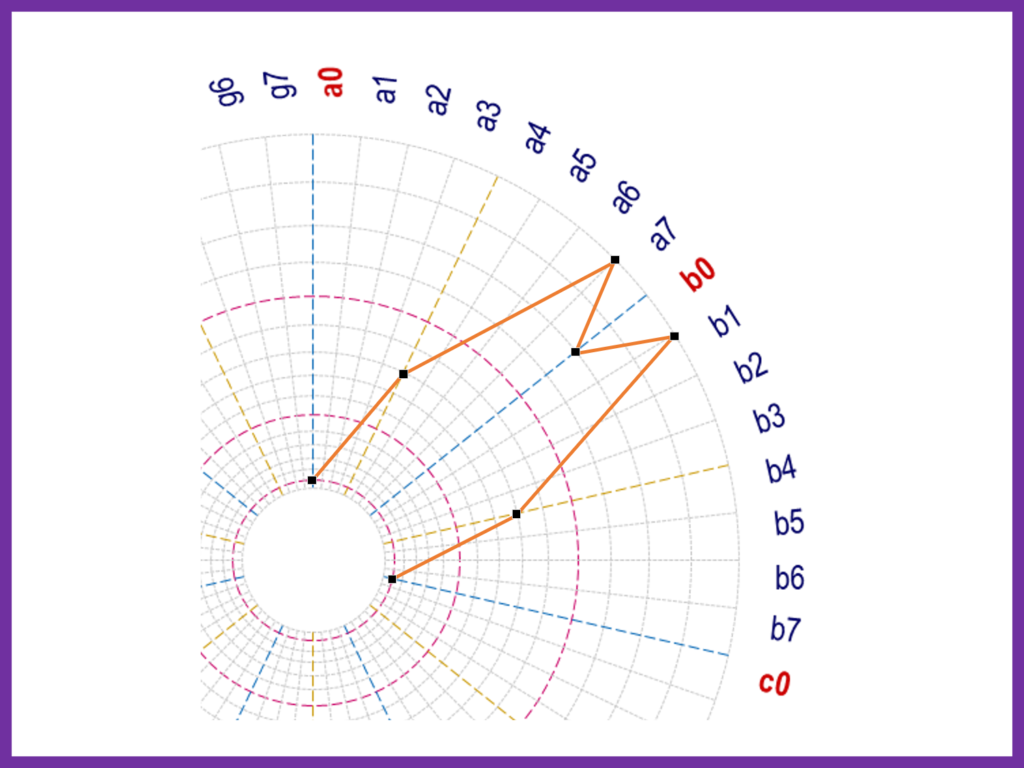
節点に使う台紙の交点はなるべくa軸以降のものを指定します
例えばa軸とg軸を混在させたコマを主軸a0を中心に描くと、角数を拡張した時にそのまま使うことが出来なくなるからです(例えば9角形に拡張しようとすると、軸記号をgからiに置き換えなければなりません)
3. コマの線分を直線から曲線に変形する
コマの各節点から伸びる方向線の端点(方向点)を調整(伸ばしたり捻ったり)して折れ線の線分を曲線に変形します
なお、図形の節点には2本の方向線が向き合って用意されていますが、普段は見ることが出来ないので、手作業で編集する場合には節点を編集状態にする必要があります
ア)方向点の強さを調整する
まず方向線の長さ(方向点の強さ)を調整します
入力フォームの強さのセルに数値(パーセント)を指定して描くと、折れ線(オレンジ)のコマを曲線(青)に変形することが出来ます
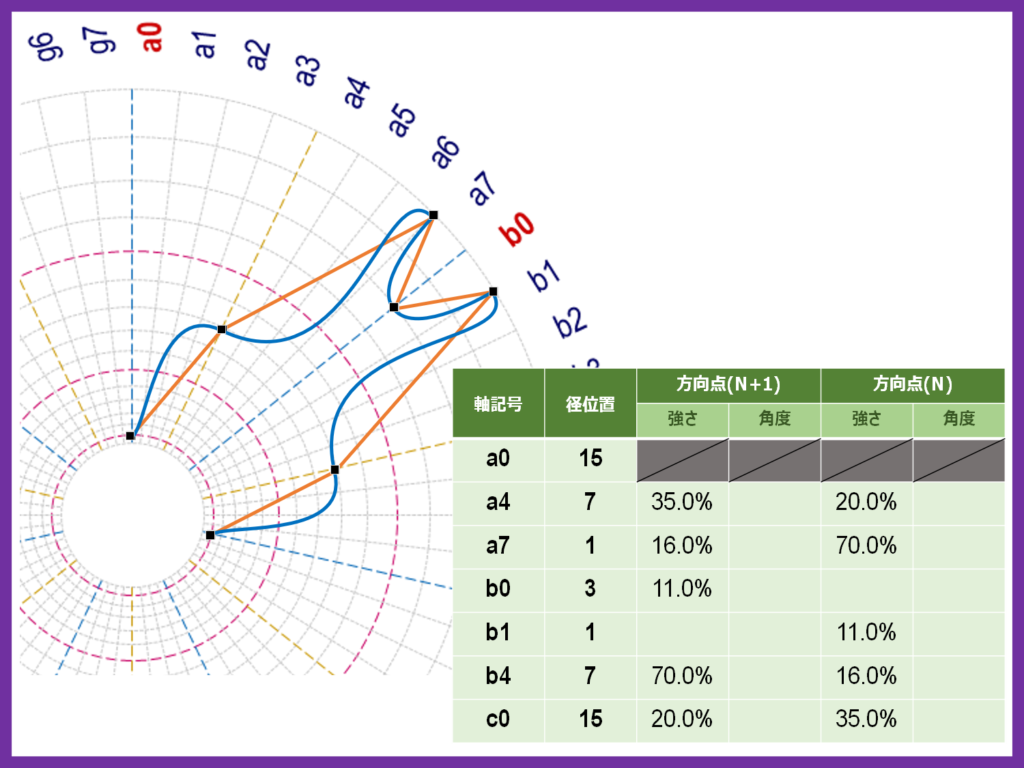
この時、方向線は各節点から該当する同心円の接線の方向に向かい合って伸ばしています
方向点の強さとして指定した数値は、その節点の中心からの長さに対する割合です
下の図で2番目の節点(a4-7)の最初の方向線(破線)の長さ(B)は、節点の中心からの長さ(A)の35%になっています
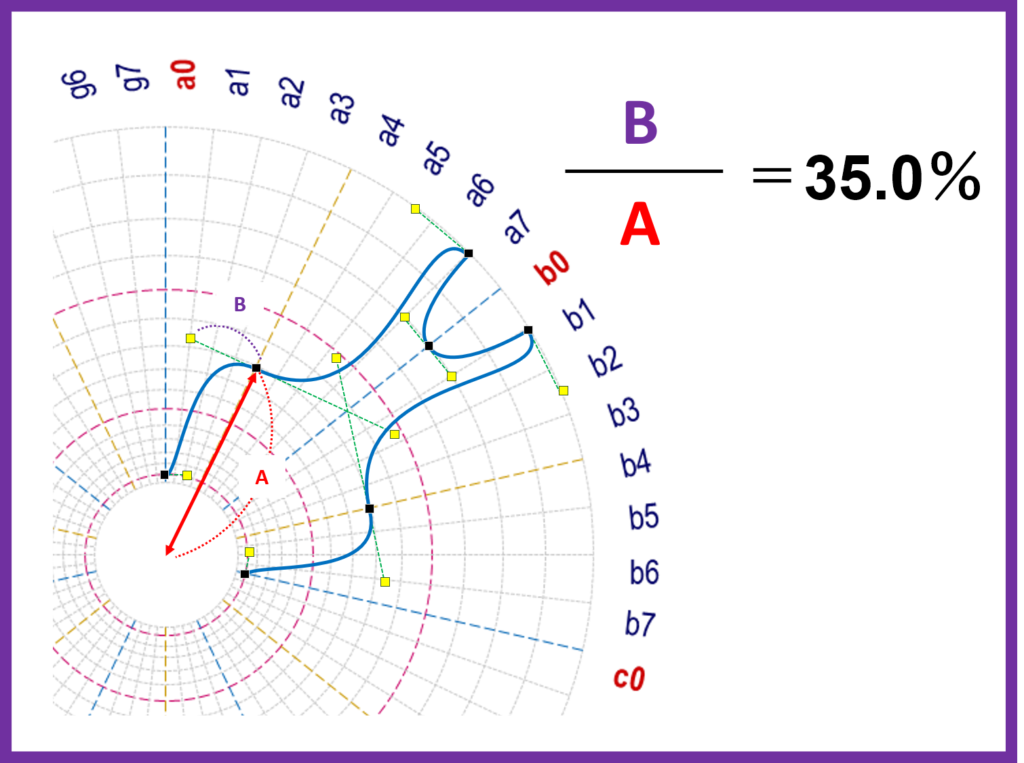
イ)方向点の角度を調整する
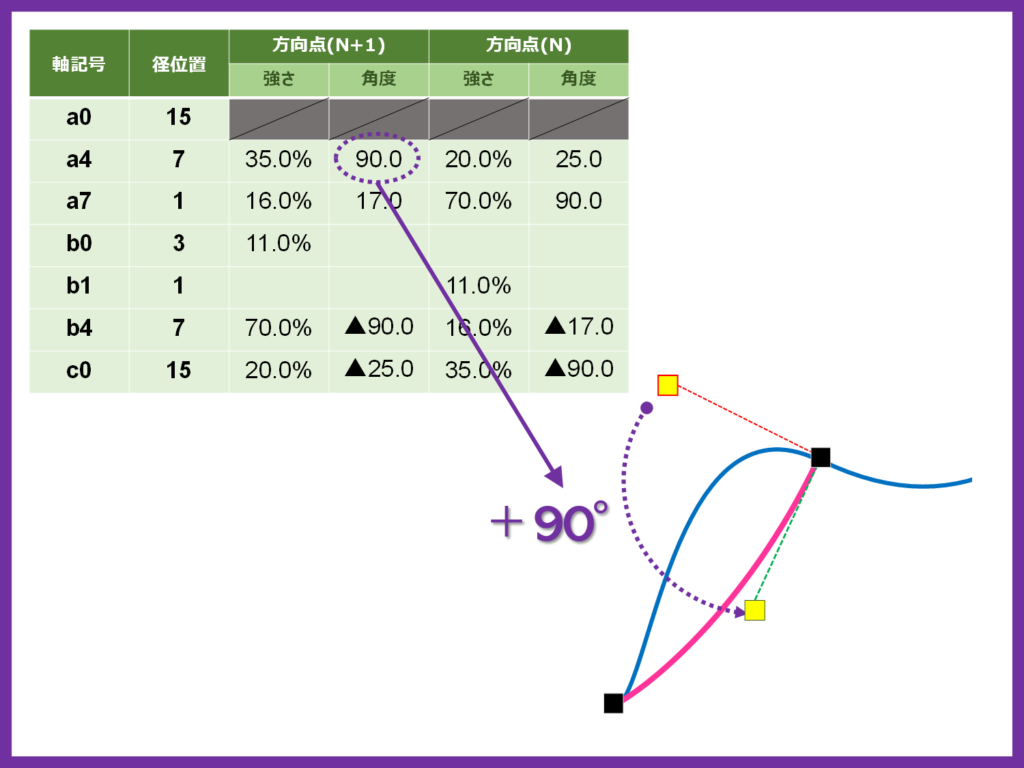
更に、この節点(a4-7)の方向点の角度に90という値を指定すると、方向線を反時計回りに90度回転させることが出来ます
方向線の向きが変わったことによって、曲線が青からピンクのように変わります
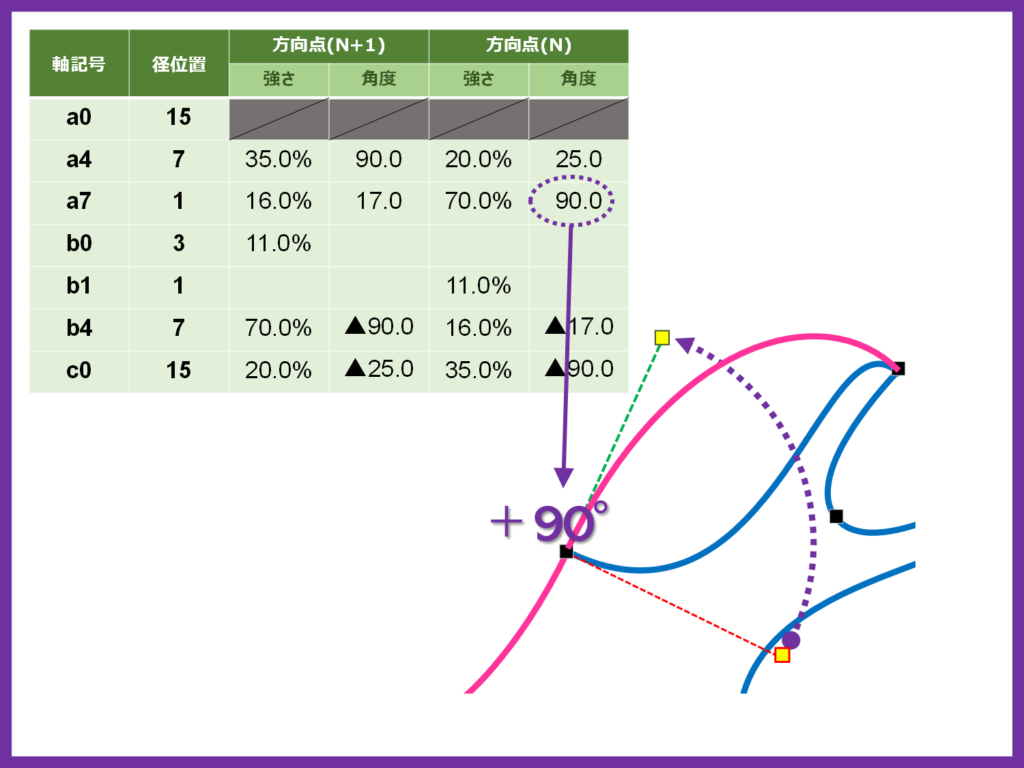
同じ節点のもう一つの方向点には、70%の強さと90の角度を指定します
強さを大きくするとカーブの引っ張り度合いが増して緩やかな曲線になります
ただし、前の方向点と同じ角度を指定しているので、引き続き向かい合った状態を保つことができるので、連結部分がスムーズな曲線に変形することが出来ます
他の節点にも角度を設定するとサンプルのコマが完成します
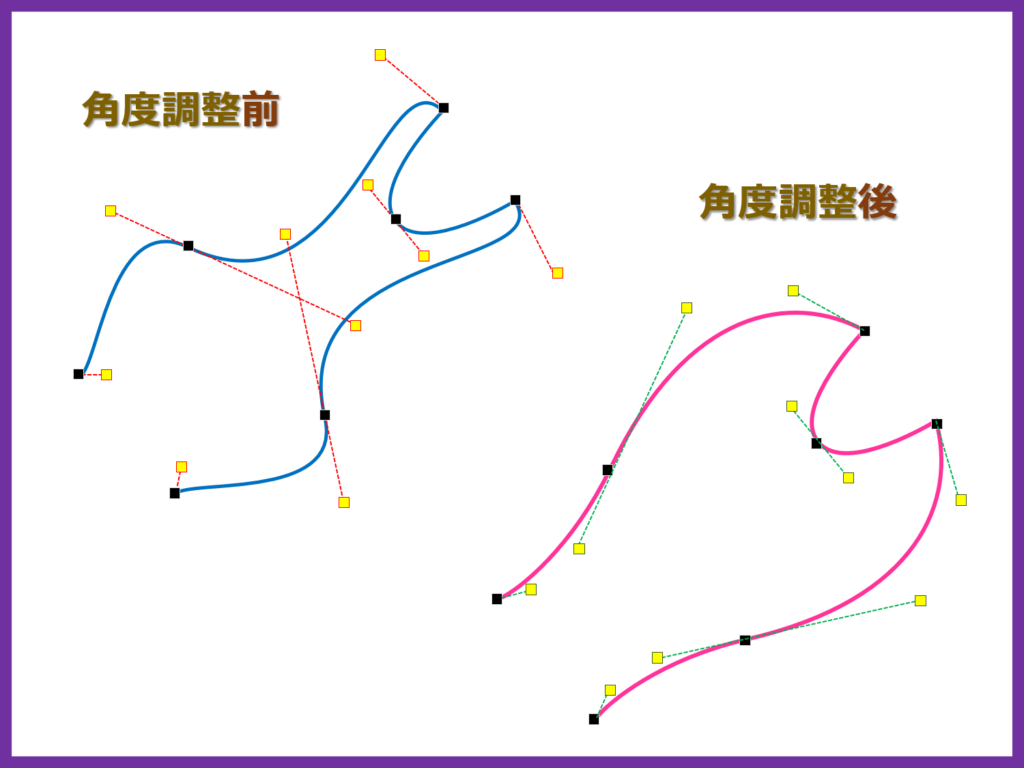
ひとつの線分の両端から伸びている方向線の、その片方の方向点に強さも角度も指定しない場合は、もう一つの方向点の調整値によって線分全体が変形するので、すべての線分の両端に方向点を配置する必要はありません
ウ)方向点の座標を計算してコマを描く
強さと角度を指定した方向点の座標も、節点の座標が分かっているので計算することができます
プログラミングで方向点の座標もパラメーターとして指定することによって、曲線のフリーフォームを描くことが出来るようになります
具体的には、キーとなるスクリプトに次のように方向点の座標を併せて記述します
…Shapes.BuildFreeform.AddNodes(最初の線分の両端の方向点の座標、2番目の節点の座標情報)
Shapes.BuildFreeform.AddNodes(2番目の線分の両端の方向点の座標、3番目の節点の座標情報)
Shapes.BuildFreeform.AddNodes(3番目の線分の両端の方向点の座標、4番目の節点の座標情報)
…
4. 多角形の頂角に応じたコマを連続してつなぎ、全体を『一筆書き』で描く
コマの描画が完成したら、続いて2番目以降の頂角の図形を描いて図形全体を完成させます
2番目以降の頂角の図形の各節点は、コマを台紙の中心を基点に一定の角度回転させた位置にあるので、その座標を計算して求めます
但し、コマの終点は次の図形の開始点になるので重複しないようにします

何度回転させるかは、コマの描き方によります
このサンプルでは、2つ先の頂角につなげているので、360÷7×2=103度が回転角度になります
図形の開始点まで連続してフリーフォームを描いて『一筆書き』の完成です

以上、簡単にフリーフォームの描き方について説明しましたが、一番労力を必要とするのは方向点の決め方です
このサンプルの場合でも、各方向点の強さと角度を最終的に決めるまで何十回と試行錯誤を重ねました
また、全体の図形のイメージは当初の考えとはかけ離れたものになることもあり、構図のパターンを偶然見つけ出すことの方が多いかも知れません
それがまた面白いところでもあります