A. 一筆書きで描くと図形全体をまとめ易くなります
このサイトで紹介する図形は、基本的には正多角形の頂点を中心とする、各頂角の範囲に基本となる図形(コマ)を描き、それぞれのコマをつなげて一本の線として仕上げています
最初のコマの開始点から線を描き始め、最後のコマの終了点が、最初のコマの開始点に重なったところで完成します
この時、一本の線が「閉じた」状態になっているので、いわゆる『一筆書き』となります
ただ、『一筆書き』という手法にこだわっているわけではなく、結果として生み出される模様の無限性を追求するのに、『一筆書き』が便利なので使っています
場合によっては、同じ線分の上を複数回通すこともありますし、単独で閉じた図形を一定の間隔をとって配置することもあるので、全ての図形が厳密にいうところの『一筆書き』ではありません
また、構図によってはコマからコマへのつながりが難しくなる場合もあるので、サポート線を使ってコマ同士をつなげて描画してから、最後にサポート線だけを削除することもあります
模様の無限性?
「メビウスの輪」をご存知でしょうか
紙一枚で無限軌道の世界が開かれます
子供のころ、初めて「メビウスの輪」を知った時の不思議な“感覚“が、今でも脳裏のどこかに残っています
実際に紙を帯状に切って、ねじって、繋げて、「メビウスの輪」を手にしたときの「どうして?」という思い、それから、帯の中心に沿って鋏を入れた時の、その結果を見たときの驚きを、今でも忘れることはありません
「クラインの壺」にも、何となく「母なる宇宙」を連想する壮大なイメージを思い描いたものです
その頃に抱いたイメージ、それは「無限」とか「連続」といった漠然としたものだったのですが、それを何とかして具体的な形にしたいとういう思いが『一筆書き』に辿り着いた理由かも知れません
身近な『一筆書き』
誰もが描いたことがある代表的な『一筆書き』に“星型”がありますが、なかなか均等な星型にならず、イライラしたこともあったのではないでしょうか
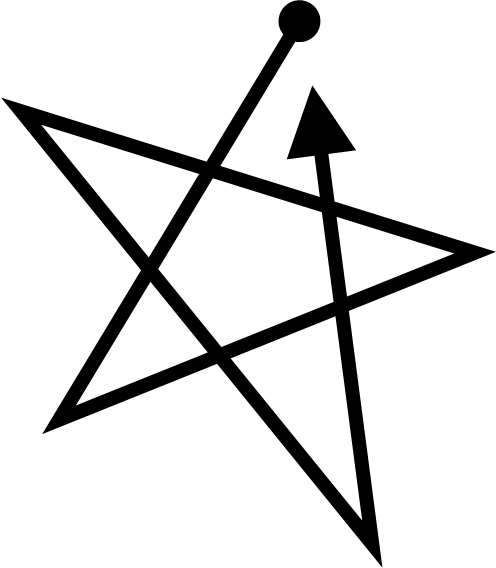
この“星型”を正五角形の頂点を結ぶように描けば、どの頂角も同じ大きさの星になります
この時のように「同じ大きさ」であることが「規律を持った幾何学模様」には欠かせません
ちょっと大げさな言い方ですが、「規律を持った幾何学模様」が完成した時、そこに連続した無限の世界が誕生します
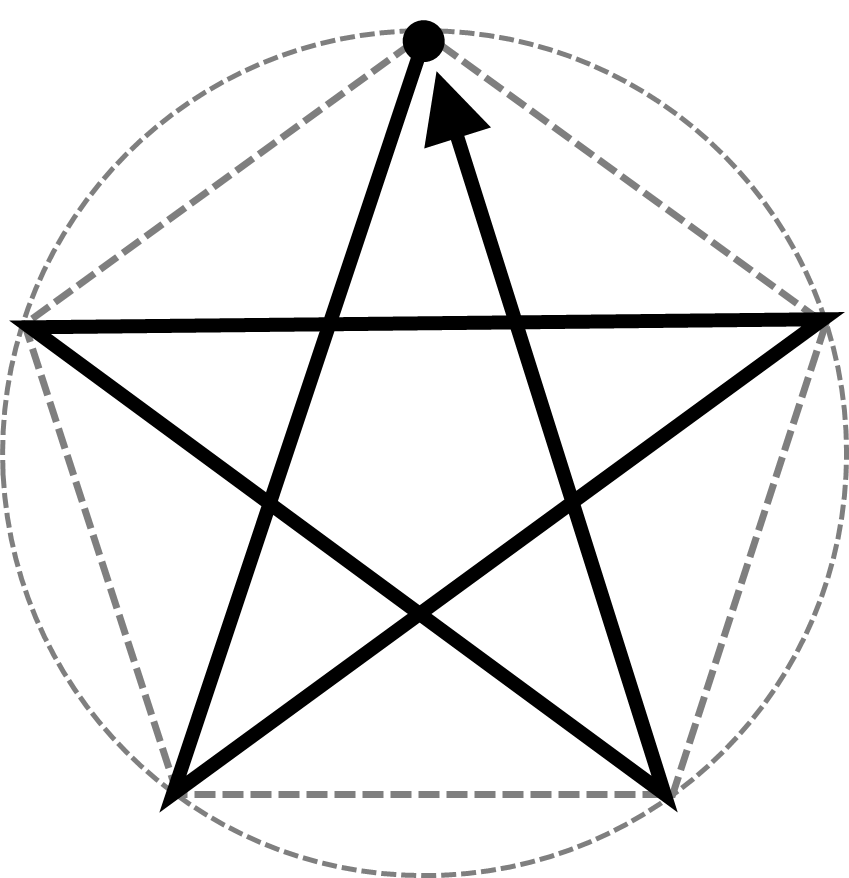
星形を『一筆書き』で描くには、もう一つ方法があります
隣り合う頂角を続けて書く方法です

最初の方法では、頂角から次の頂角に伸ばす直線の方向、言い換えれば正多角形の角数によって、頂角の角度が決まってしまいます
頂角の角度を自由に決めることが出来れば、図形として自由度が増しますし、描く順番も、隣り合う頂角を連続して描くので、角数が増えても、ルールをシンプルに決めることが出来ます

角数を増やした時にも、線分同士が込み合わずに、すっきりした図形に仕上げることが出来るので、図形のコンセプトを主張し易くなります
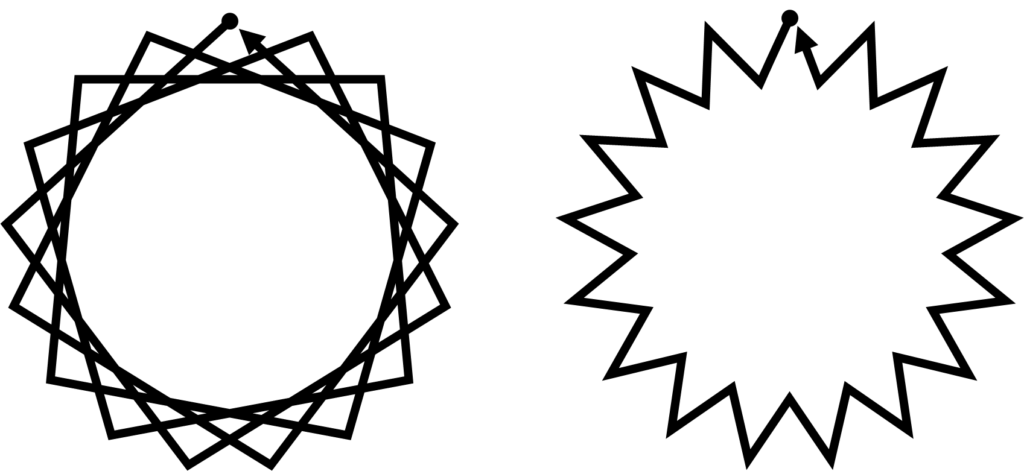
サンプルとして正17角形の星形を、二つの方法で描画したときの結果を比べてみてください
一筆書きは格子柄
『一筆書き』で描いた図形は簡単に格子柄になります
