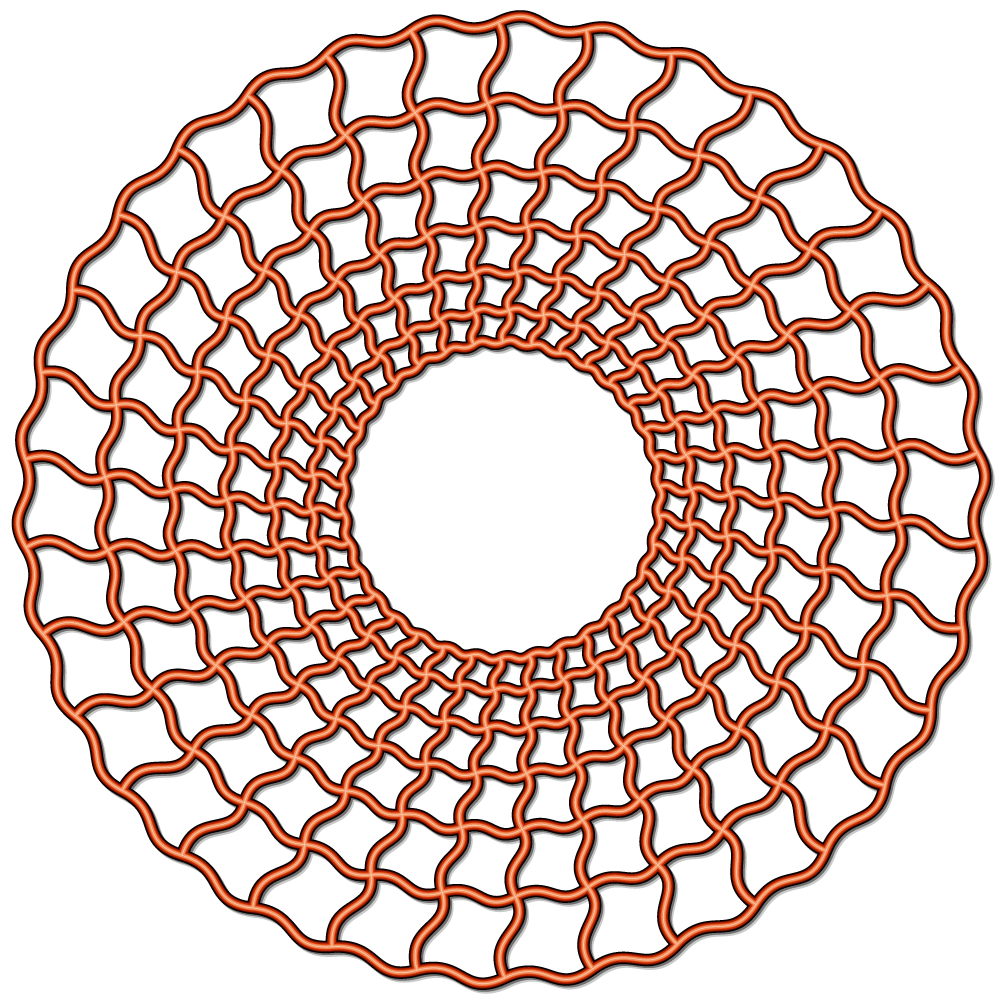
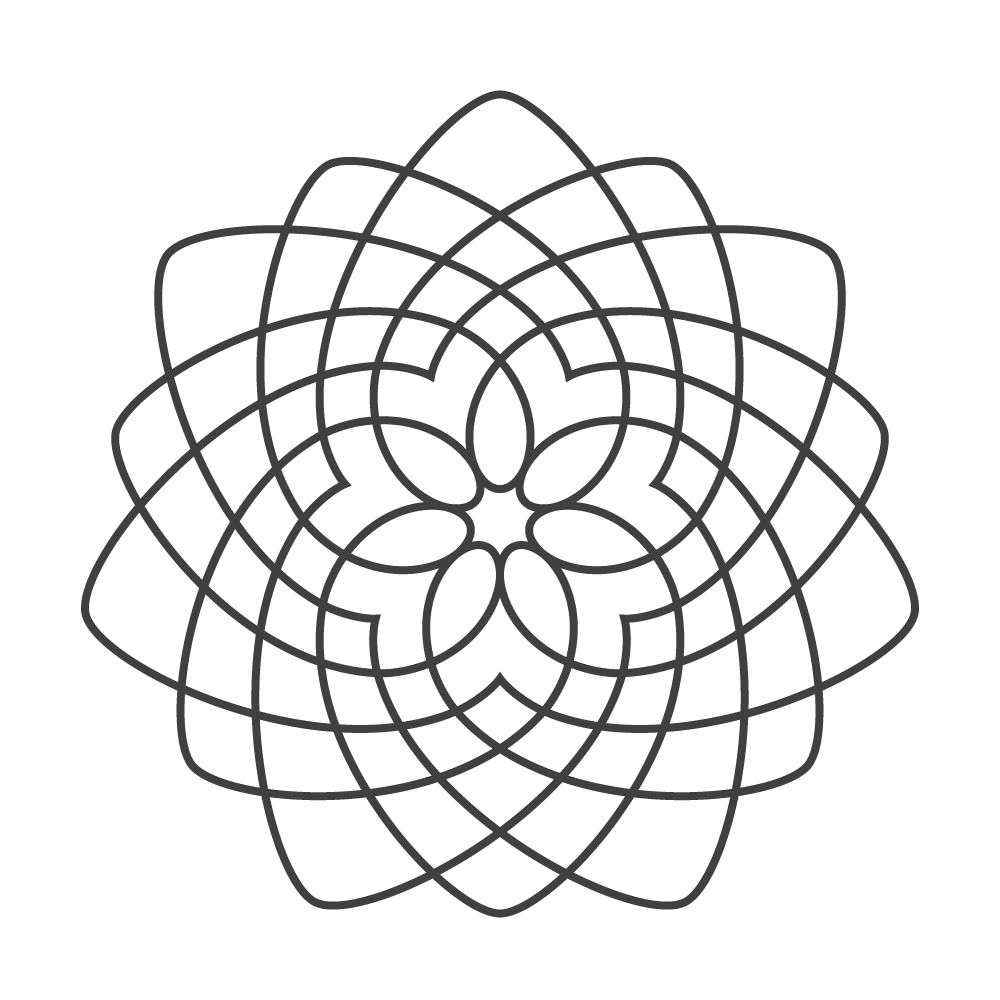
日本古来のパターン模様である和柄をモチーフとした作品(wagara001)を「和柄グループ」に登録しました
和柄のコマとなる図形は誰もが一度は目にしたことのあるもので、その中から代表的な千鳥格子の一種を最初の作品として取り上げました
和柄は同じ図形が2次元の平面に展開されているところが特徴であり、M.C.エッシャーのだまし絵と似ているところがあります
騙すというよりは、平面の広がりの中に誘い込むような魅力に溢れていると思います
ただ、平面の大きさにその世界がとどまらざるを得ないので、無限性を求めるには限界がある一方、円盤上に展開することによってまた面白い世界観を築くことが出来そうです
今回参考にした和柄は、波線を縦横に交差させた格子柄で、図柄としては単純な構図となっています
パターンを構成する基本図形も小さいものなので、角数は増える傾向にあり、今回も34角の多角形がベースとなっています
コマは2つの頂角をカバーしているので、作業としては17角形の図形の描画と同じになりました
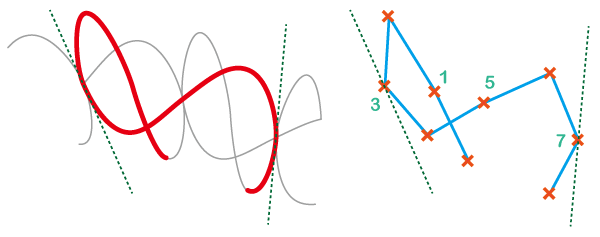
今回の作品の線描の骨格は下図の通りです(赤い線がコマです)
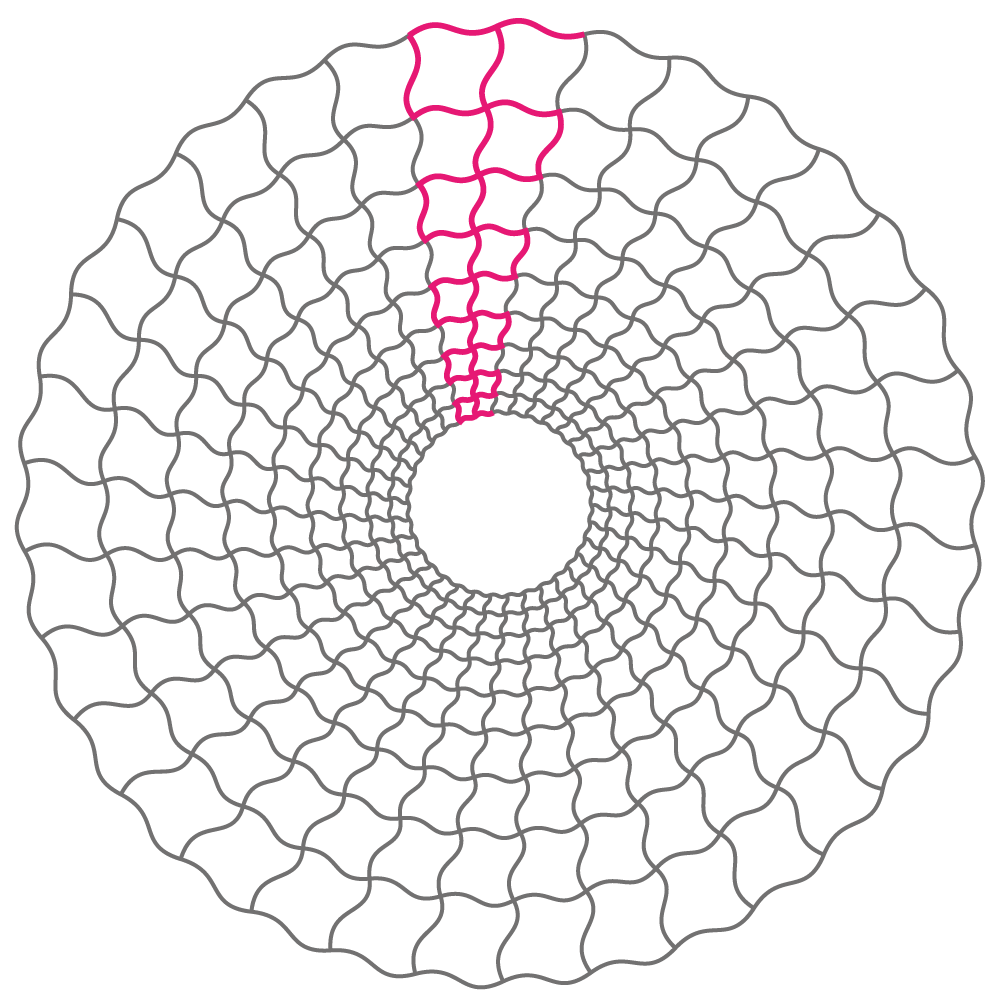
このコマの波線の曲がり具合を決定する過程で、思ってもいなかった図形もできたので、その図形も紹介したいのですが、まずは波線の曲がり具合について、曲げ具合の強弱で変わる様子をサンプルでご紹介します
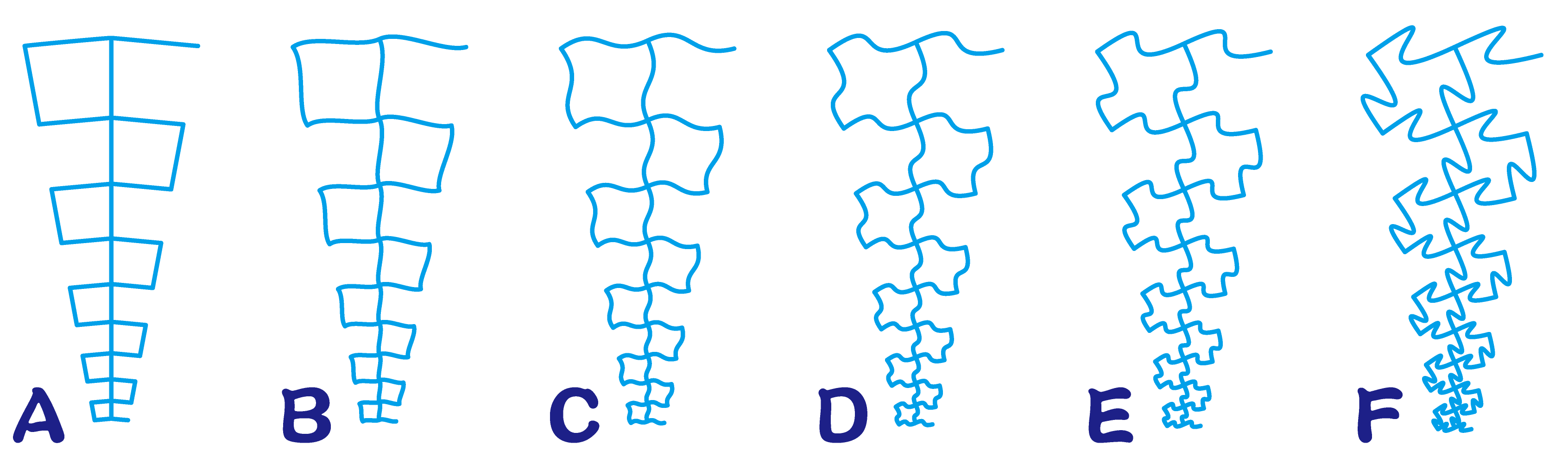
最終的にはCのコマを採用しているのですが、作業としてはAのように直線で正方形を円盤状に配置するところから始めています
線分がS字状になるように方向点を調整しているのですが、曲げの強度に応じてコマのパターンが変形して行きます
F以上に曲げてしまうと線分同士が重なり始めるので、Fくらいが限界でした
どのような図形に仕上がるのか、結果が分かるようにB、DとFのケースでサンプルを作ってみました

コマに捻りを入れる
次の工程で構図全体に流れる動きを入れるために、渦巻き状の捻りを入れます
具体的には、図形の中心から離れるにつれて元の位置から円周上をスライドさせています
スライドの大きさによってコマのイマージが下記のサンプルのように変わります
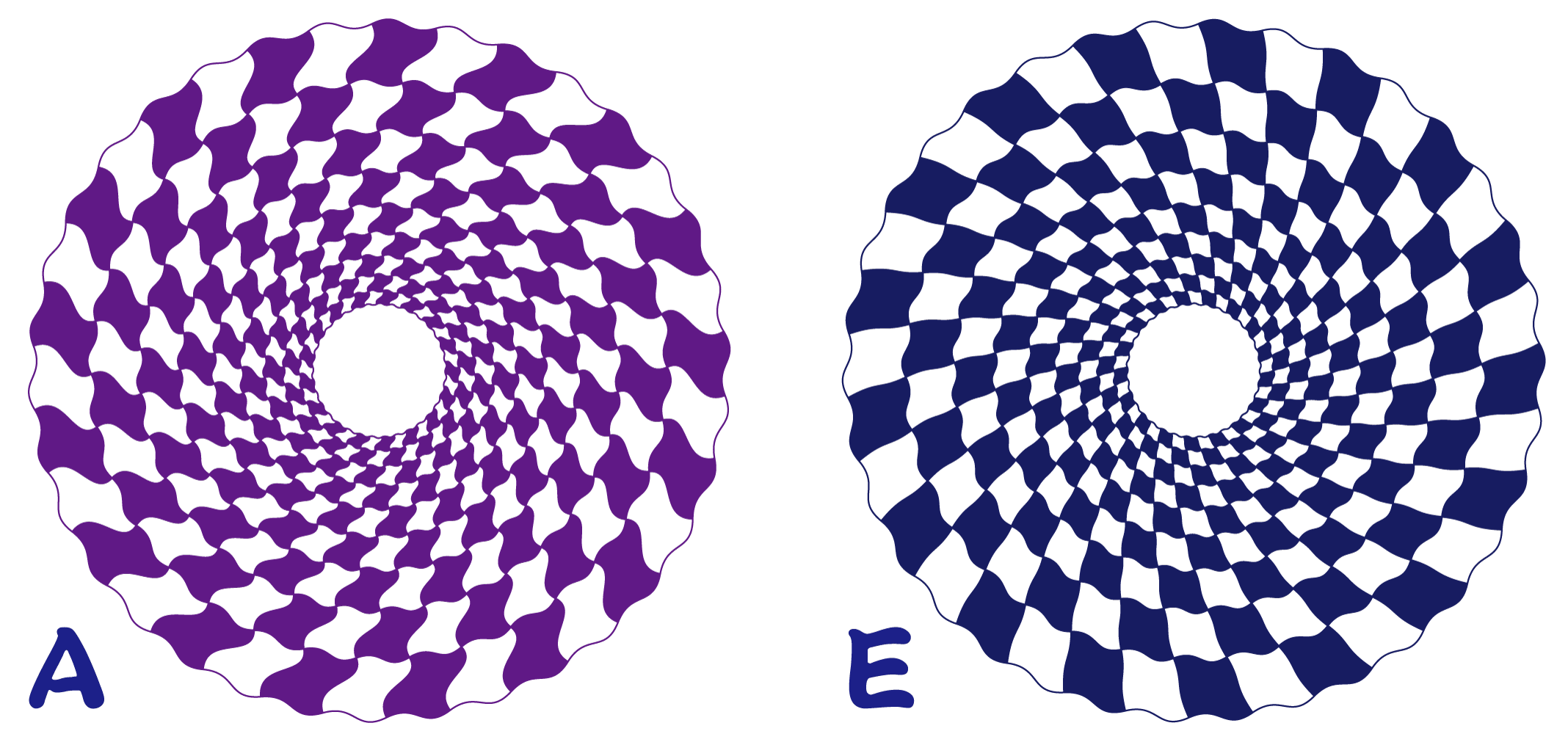
AからCは時計回りの方向に、DからFは反対方向にスライドさせています
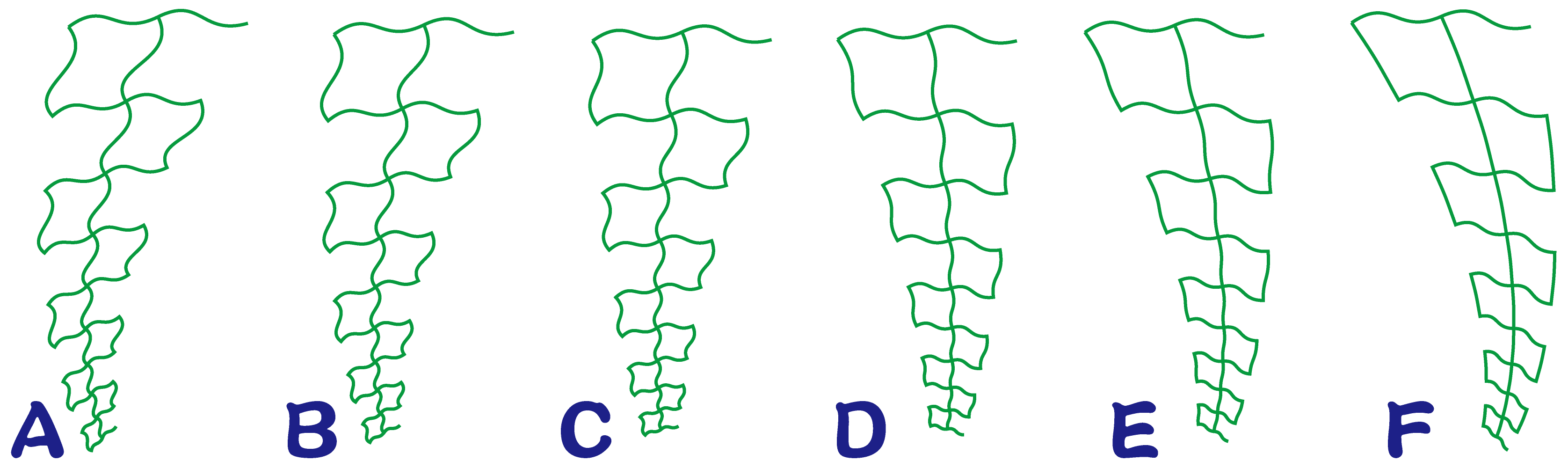
どのような図形に仕上がるのか、結果が分かるようにAとEのケースでサンプルを作ってみました
サポート線を活用する
この作品を仕上げる過程で、一筆書きで一気に閉じた図形を作成するために、一旦サポート線を含んだコマを作成し、完成後サポート線を削除しています
今回の図形はコマの節点が35個あるので、全体では(35-1)×17=578個の節点を持っています
全ての節点から方向線を伸ばしているので、更に1,156個の方向点を指定しています
これだけの点を持つ図形を精緻な模様として描くためには、閉じた図形として一気に仕上げる必要があり、例えば、17個のコマを360÷17度ずつ回転させながら接合させていく方法も考えられるのですが(実際やってみて挫折しましたが)、全ての点をあるべき場所に正確に配置することは簡単ではありません
最近の描画ソフトは、回転や繰り返しなどの機能が使いやすくなっているので、大きなコマであれば、おおよその位置に配置することもできるのですが、和柄の様なパターンではうまくいきませんでした
かといって、全ての点の座標を細かく指定するのも1000を超えるケースとなると生産性が極度に落ちてしまいます
このような理由から、後工程で削除という作業が発生しますが、サポート線を活用する方法を採用しています
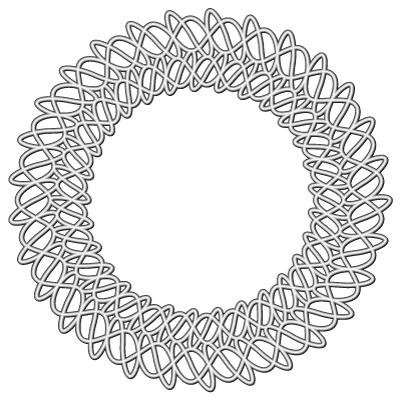
以下のコマがサポート線(赤線)を含んだ原型です
一筆は右上の丸から始まり、右下の矢印で次のコマにつながっています
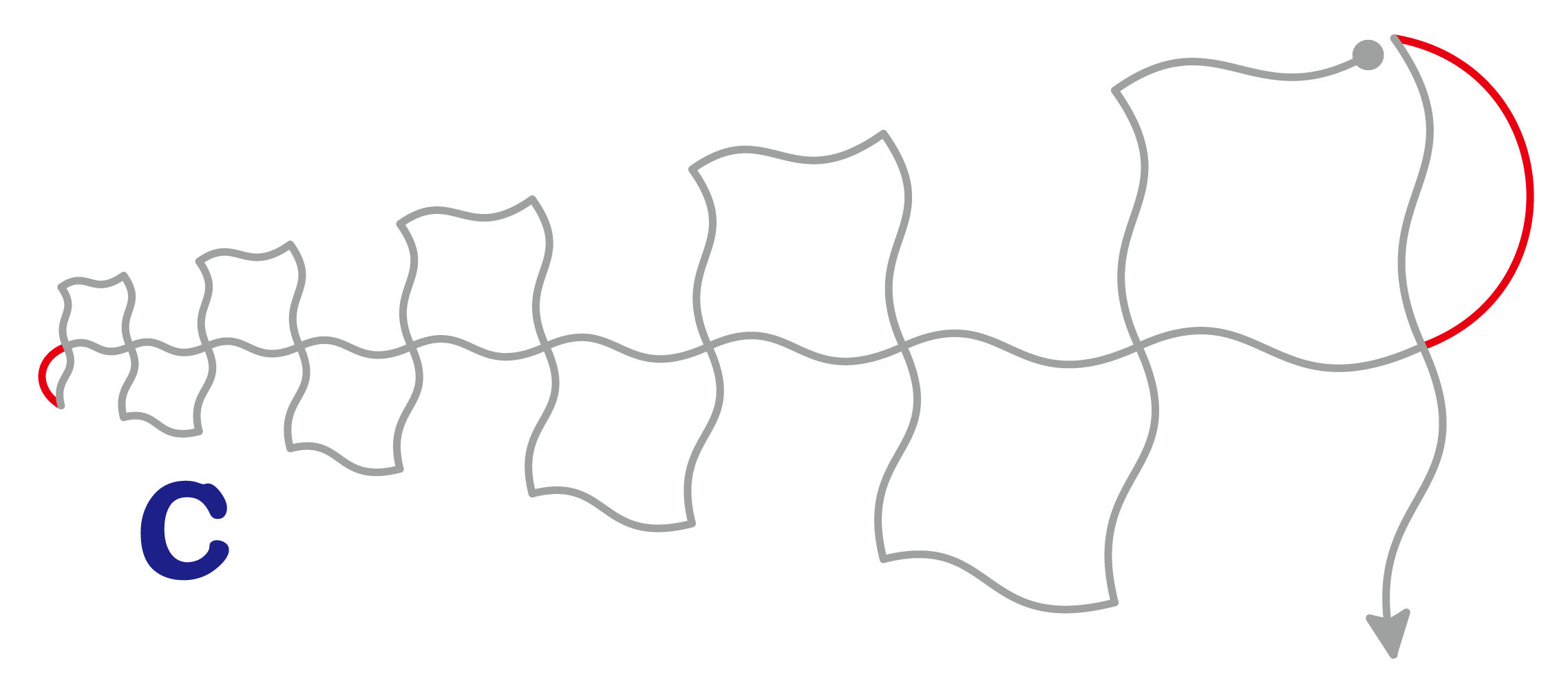
仕上げ
朱色を基調とした色合いにし、外側から内側に向けて濃度を落としてグラデーションの効果を狙いました
外周は格子のコンセプトを活かすために外枠で囲んであります
出来上がって気づいたのですが、なぜか渦巻のように中心に流れる動きを感じます

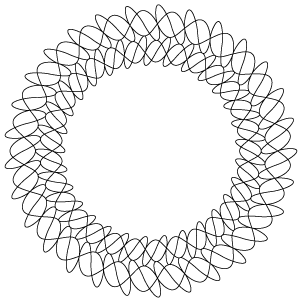
最後にバリエーションのひとつとしてスケルトンタイプの図形を紹介します
立体的な骨格の構造に見えるように、線の太さを段階的に変えた4つの図形を重ねて描いています